미적분 값 계산하기

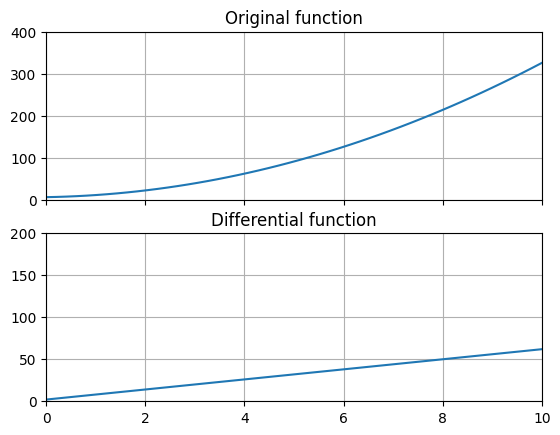
함수의 미분

EX1_function_differential.py

import matplotlib.pyplot as plt
import numpy as np


def f(x):
    return 3 * x ** 2 + 2 * x + 6


def g(func, x):
    y = []
    h = 0.01
    for _x in x:
        y.append((func(_x + h) - func(_x)) / h)
    return np.array(y)


if __name__ == "__main__":
    x = np.linspace(0, 10)
    ax1 = plt.subplot(2, 1, 1)
    ax1.set_title("Original function")
    ax1.set_xlim(0, 10)
    ax1.set_ylim(0, 400)
    ax1.axes.xaxis.set_ticklabels([])
    ax1.plot(x, f(x))
    ax1.grid(True)
    ax2 = plt.subplot(2, 1, 2)
    ax2.set_title("Differential function")
    ax2.set_xlim(0, 10)
    ax2.set_ylim(0, 200)
    ax2.plot(x, g(f, x))
    ax2.grid(True)
    plt.savefig("EX1_function_differential.png", bbox_inches='tight')

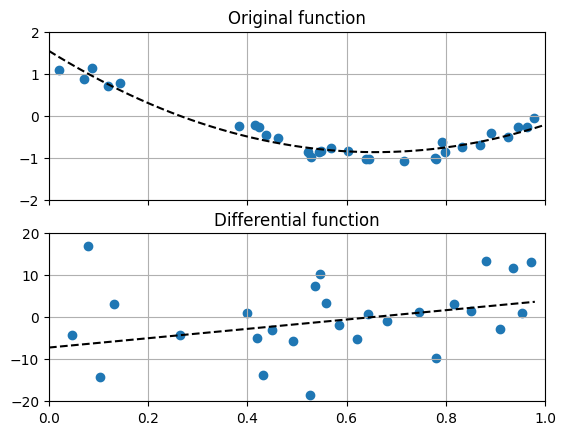
데이터의 미분량

EX2_data_differential.py

import os

os.chdir(os.path.abspath(os.path.dirname(__file__)))

"""데이터의 미분량
소스코드의 실행 디렉토리와 데이터파일의 디렉토리가 일치하도록 조정
"""
import numpy as np
import matplotlib.pyplot as plt

x = []
y = []

with open("data.csv", "r") as f:
    for line in f.readlines():
        _x, _y = [float(i) for i in line.split(" ")]
        x.append(_x)
        y.append(_y)


def g(x, y):
    new_x = []
    new_y = []
    for idx in range(len(x) - 1):
        new_x.append((x[idx] + x[idx + 1]) / 2)
        new_y.append((y[idx + 1] - y[idx]) / (x[idx + 1] - x[idx]))
    return new_x, new_y


if __name__ == "__main__":
    fit = np.poly1d(np.polyfit(x, y, 2))
    fit_x = np.linspace(0, 1)
    fit_y = fit(fit_x)

    # 그래프 1: 원시데이터
    ax1 = plt.subplot(2, 1, 1)
    ax1.set_title("Original function")
    ax1.set_xlim(0, 1)
    ax1.set_ylim(-2, 2)
    ax1.axes.xaxis.set_ticklabels([])
    ax1.plot(fit_x, fit_y, "k--")
    ax1.scatter(x, y)
    ax1.grid(True)

    # 그래프 2: 미분한 데이터
    ax2 = plt.subplot(2, 1, 2)
    ax2.set_title("Differential function")
    ax2.set_xlim(0, 1)
    ax2.set_ylim(-20, 20)
    ax2.plot(fit_x[:-1], np.diff(fit_y) / (fit_x[1] - fit_x[0]), "k--")
    ax2.scatter(*g(x, y))
    ax2.grid(True)

    plt.savefig("EX2_data_differential.png", bbox_inches='tight')

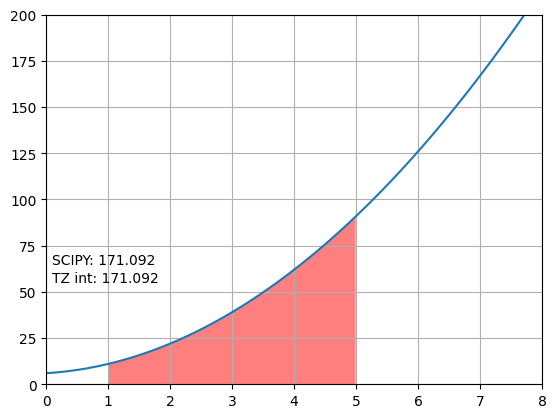
함수의 적분

EX3_function_integration.py

import os
os.chdir(os.path.abspath(os.path.dirname(__file__)))

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import trapezoid

h = 0.01
min_x = 1
max_x = 5


def f(x):
    return 3 * x ** 2 + 2 * x + 6


def int_f(func, x_min, x_max, h):
    output = 0
    x = np.arange(x_min, x_max, h)
    for idx in range(len(x) - 1):
        output += (func(x[idx]) + func(x[idx + 1])) * h / 2
    return output


if __name__ == "__main__":
    x = np.linspace(0, 8)
    x_inf = np.arange(min_x, max_x, h)
    y_inf = f(x_inf)
    x_inf = np.concatenate(([x_inf[0]], x_inf, [x_inf[-1]]))
    y_inf = np.concatenate(([0], y_inf, [0]))

    plt.plot(x, f(x))
    plt.fill(x_inf, y_inf, "r", alpha=0.5)
    plt.text(0.1, 55, f"TZ int: {int_f(f, min_x, max_x, h):.3f}")
    plt.text(0.1, 65, f"SCIPY: {trapezoid(f(x_inf), x_inf, h):.3f}")
    plt.grid(True)
    plt.xlim(0, 8)
    plt.ylim(0, 200)
    plt.savefig("EX3_function_integration.png", bbox_inches='tight')

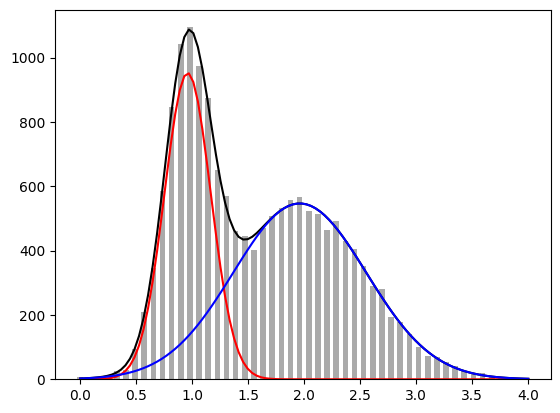
데이터의 적분

EX4_data_integration.py

import os
os.chdir(os.path.abspath(os.path.dirname(__file__)))

import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import curve_fit
from scipy.integrate import trapezoid

# 데이터 읽어들이기
bins, count = [], []
with open("hist_data.csv", "r") as f:
    for line in f.readlines():
        _b, _c = [float(i) for i in line.split(",")]
        bins.append(_b)
        count.append(_c)

# 모델 함수
def particle(x, a, b, c):
    return a * np.exp(-((x - b) ** 2) / (2 * c ** 2))


def model(x, a_0, a_1, a_2, a_3, a_4, a_5):
    p_a = particle(x, a_0, a_1, a_2)
    p_b = particle(x, a_3, a_4, a_5)
    return p_a + p_b

if __name__ == "__main__":
    popt, pcov = curve_fit(model, bins, count, p0=[100, 1, 0.1, 100, 4, 0.1])
    xdata = np.linspace(0, 4, 100)

    print(popt)

    p_a_value = trapezoid(particle(xdata, *popt[:3]), xdata)
    p_b_value = trapezoid(particle(xdata, *popt[3:]), xdata)

    print(f"Particle A: {p_a_value:.2f}")
    print(f"Particle B: {p_b_value:.2f}")
    print(f"Proportion particle data (A/B): {p_a_value/p_b_value:.3f}")
    print(f"Proportion particle reference (A/B): {6000/10000:.3f}")

    plt.plot(xdata, model(xdata, *popt), "k")
    plt.plot(xdata, particle(xdata, *popt[:3]), "r")
    plt.plot(xdata, particle(xdata, *popt[3:]), "b")
    plt.bar(bins, count, 0.05, color="#AAA")
    plt.savefig("EX4_data_integration.png", bbox_inches='tight')